Zachęcony dyskusją na oficjalnym news serwerze Rhino oraz ciągłą potrzebą dążenia użytkowników do doskonałości, proponuję pewien trick, który pozwoli budować optymalne (czyli w skrócie - najprostsze jak się da) powierzchnie. Każda dodatkowa isoparma na powierzchni złożonej zawsze wiąże się z dodatkowymi węzłami, co również przekłada się na moc komputera, która potrzebna jest, aby taką powierzchnię wyświetlić. Innymi słowy, im bardziej będziemy starali się zachować jak najprostszą geometrię - tym bardziej skomplikowany model uda nam się odwzorować. Druga sprawa, to fakt, że im prostsza geometria - tym "łatwiej" i bezbłędnie działają na niej najróżniejszego rodzaju funkcje i komendy Rhino, łącznie z transformacjami.
Rhino, niestety, za pomocą wbudowanych swoich narzędzi, nie generuje optymalnych powierzchni. Taka jest prawda. Owszem, za ich pomocą da się oddać każdy kształt, połączyć go z innym i cieszyć się efektem, ale dobrym nawykiem jest zawsze optymalizacja geometrii, która czasami pochłania więcej czasu, niż samo modelowanie.
Prosty przykład (mocno inspirowany z dyskusji na serwerze newsów McNeela).
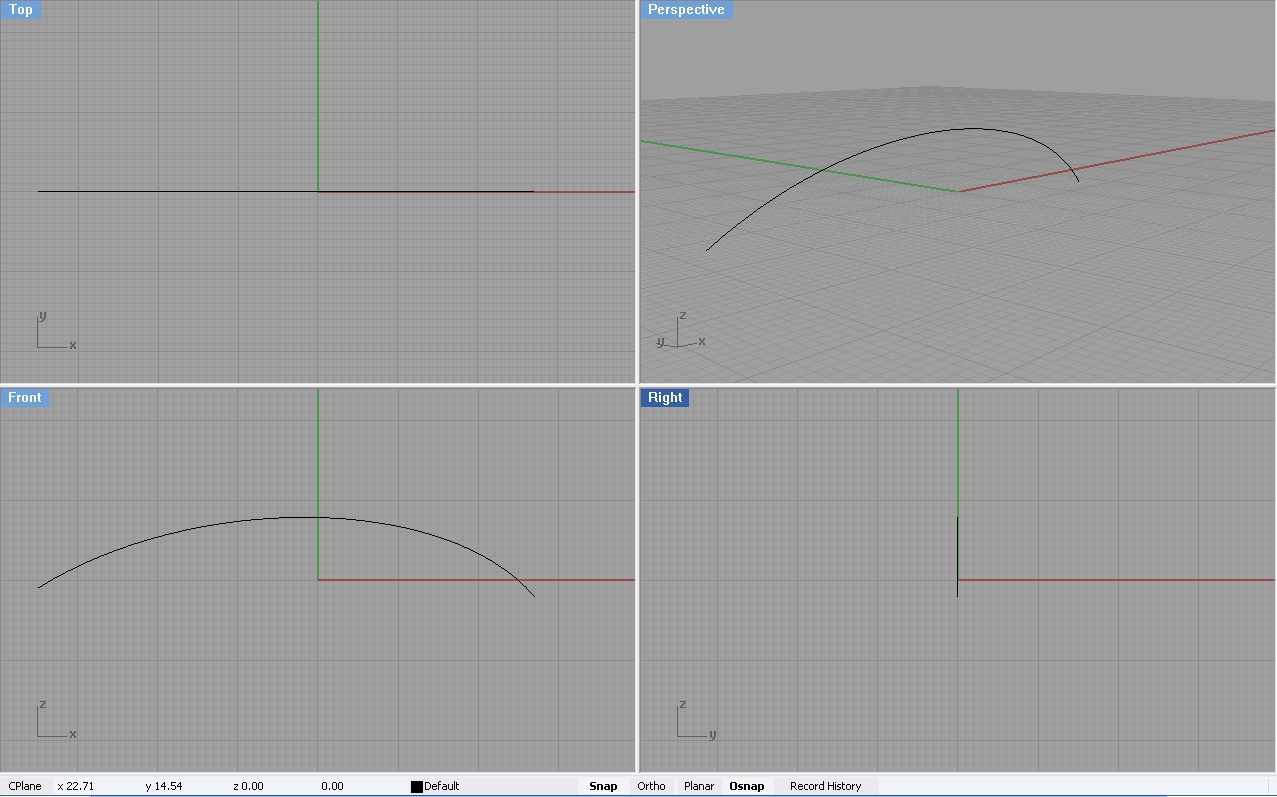
3 krzywe - przygotowane pod komendę Sweep 1 Rail. Jedna krzywa to ścieżka, druga i trzecia, to "przekroje".
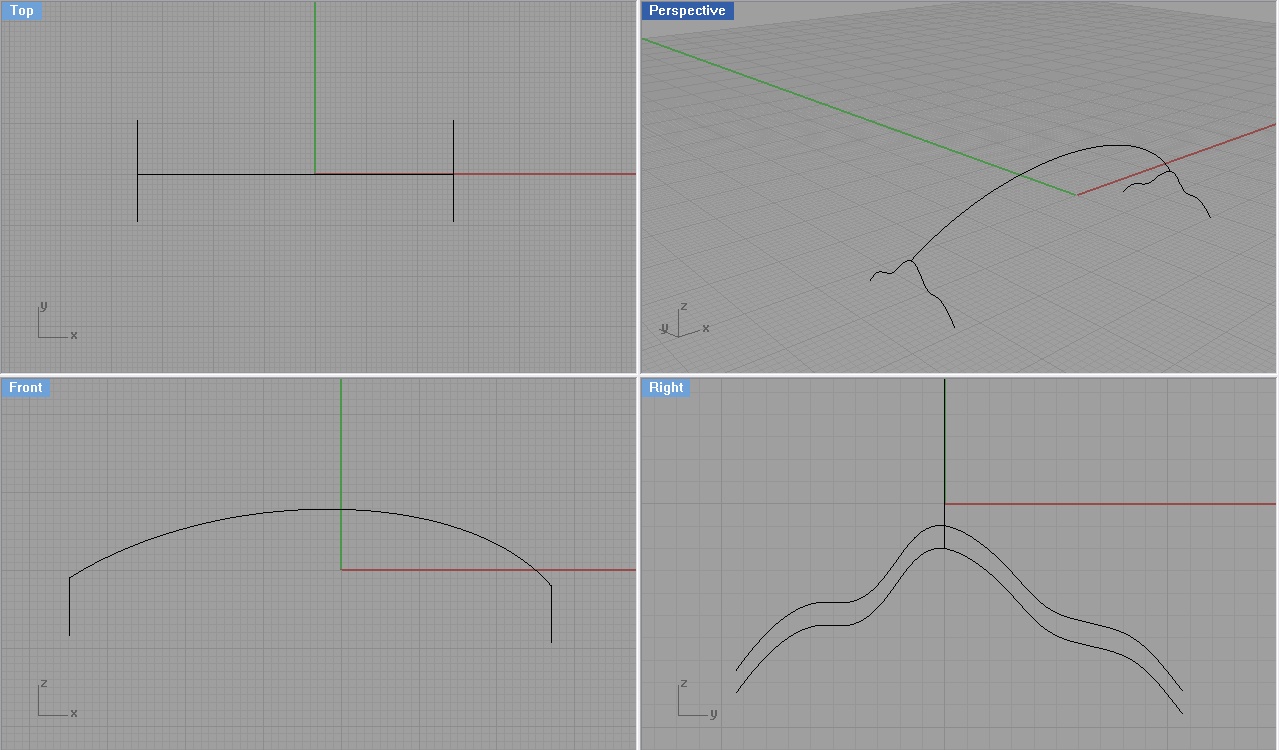
Uruchamiamy bardzo często używaną komendę Sweep (Menu Surface - > Sweep 1 Rail)
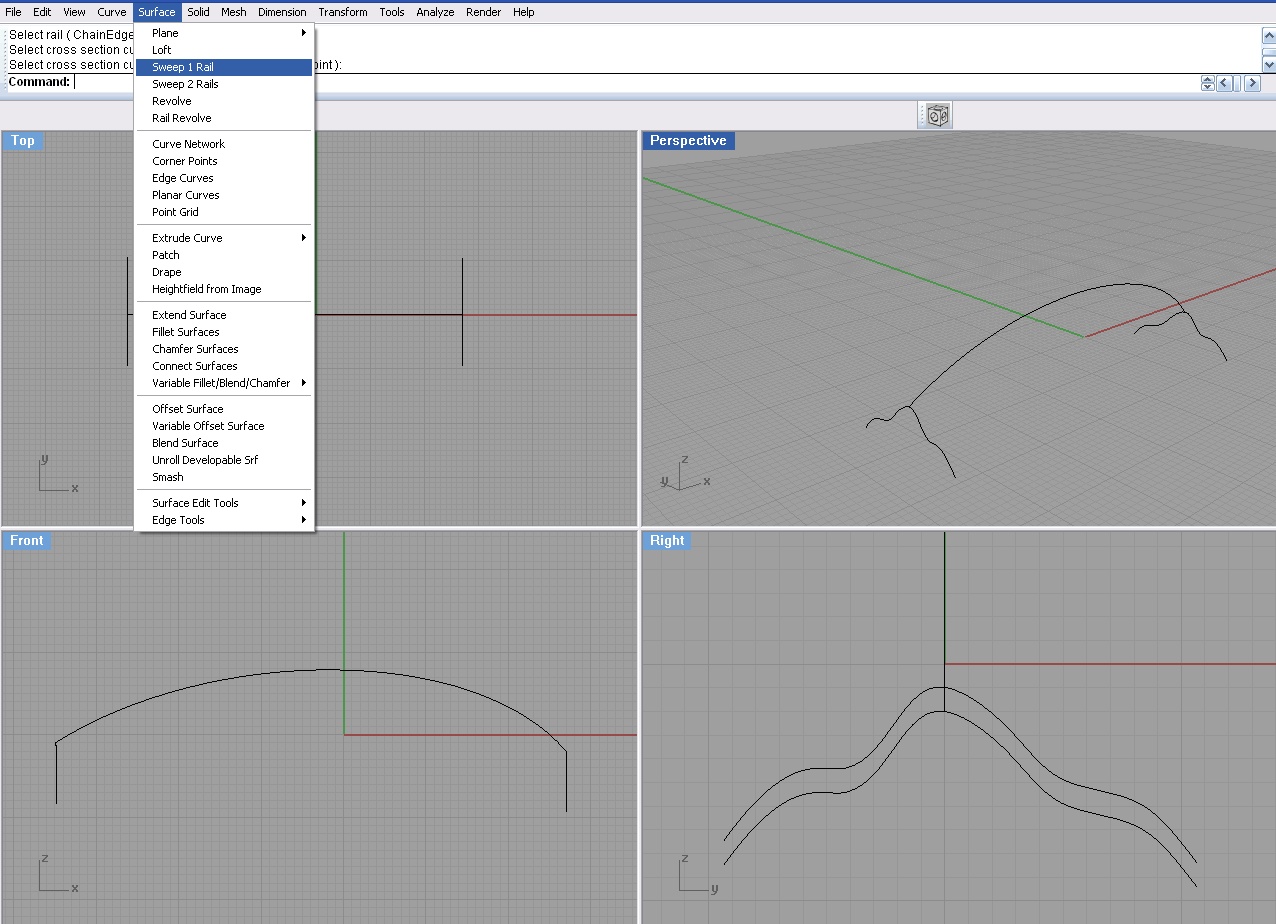
Podajemy krzywą ścieżkę i profile.
Oczywiście zadziałało prawidłowo. Niestety geometria jest bardzo gęsta, za gęsta jak na optymalną.
Co na to poradzić ? Przebudować całą powierzchnię z określoną, mniejszą ilością isoparm? Eee, nie, to nie gwarantuje efektu i czasami może nam zmienić kształt powierzchni. Zastosujemy "sztuczkę - magiczkę"
NURBS jest bardzo obiektową geometrią, powierzchnie tworzy się w nich w dokładni taki sam sposób, jak krzywe, co więc stanie się, jak umieścimy nasz profil w punktach kontrolnych, które tworzą samą naszą krzywą - ścieżkę? Włączamy Punkty kontrolne na krzywej - ścieżce i do dzieła.
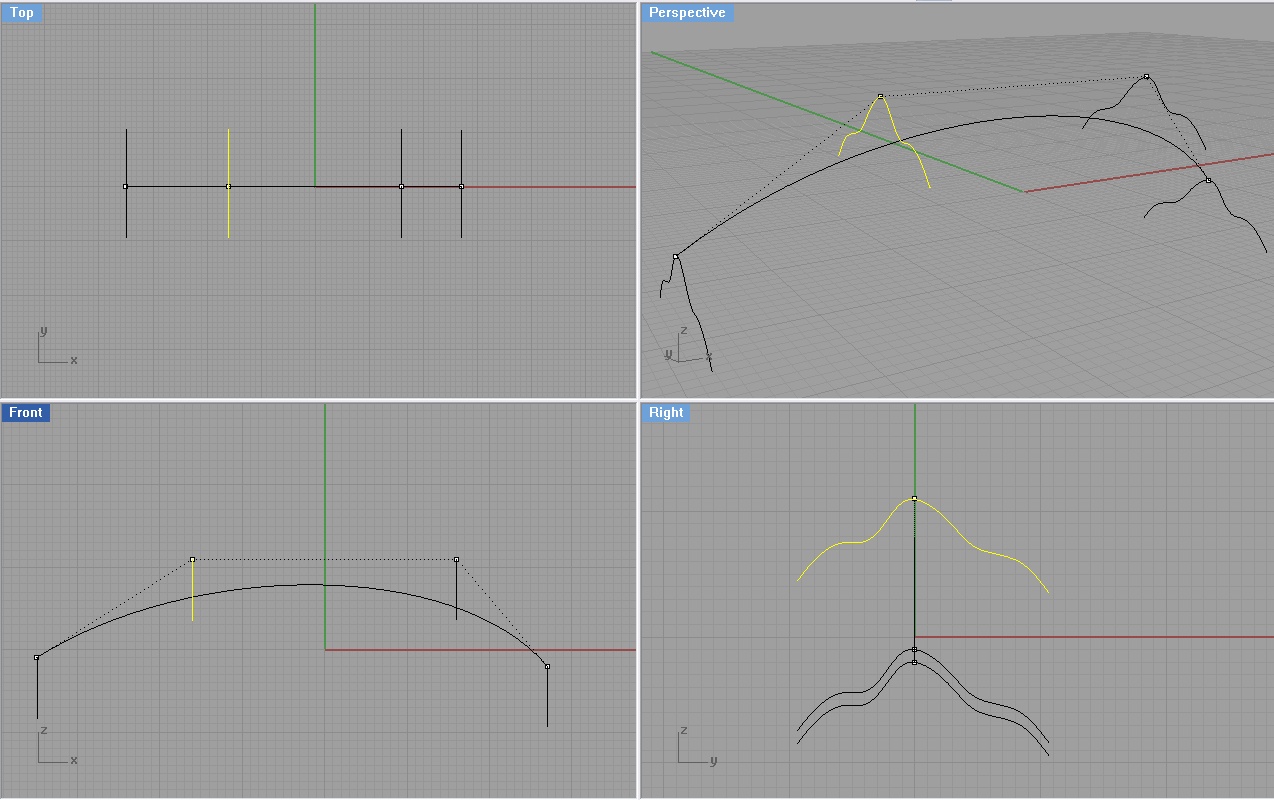
Dziwnie to wygląda... I co teraz znowu sweep?
Otwórz nie - zwykły loft ( Meru Surface -> Loft), ale z opcją opcją Loose.
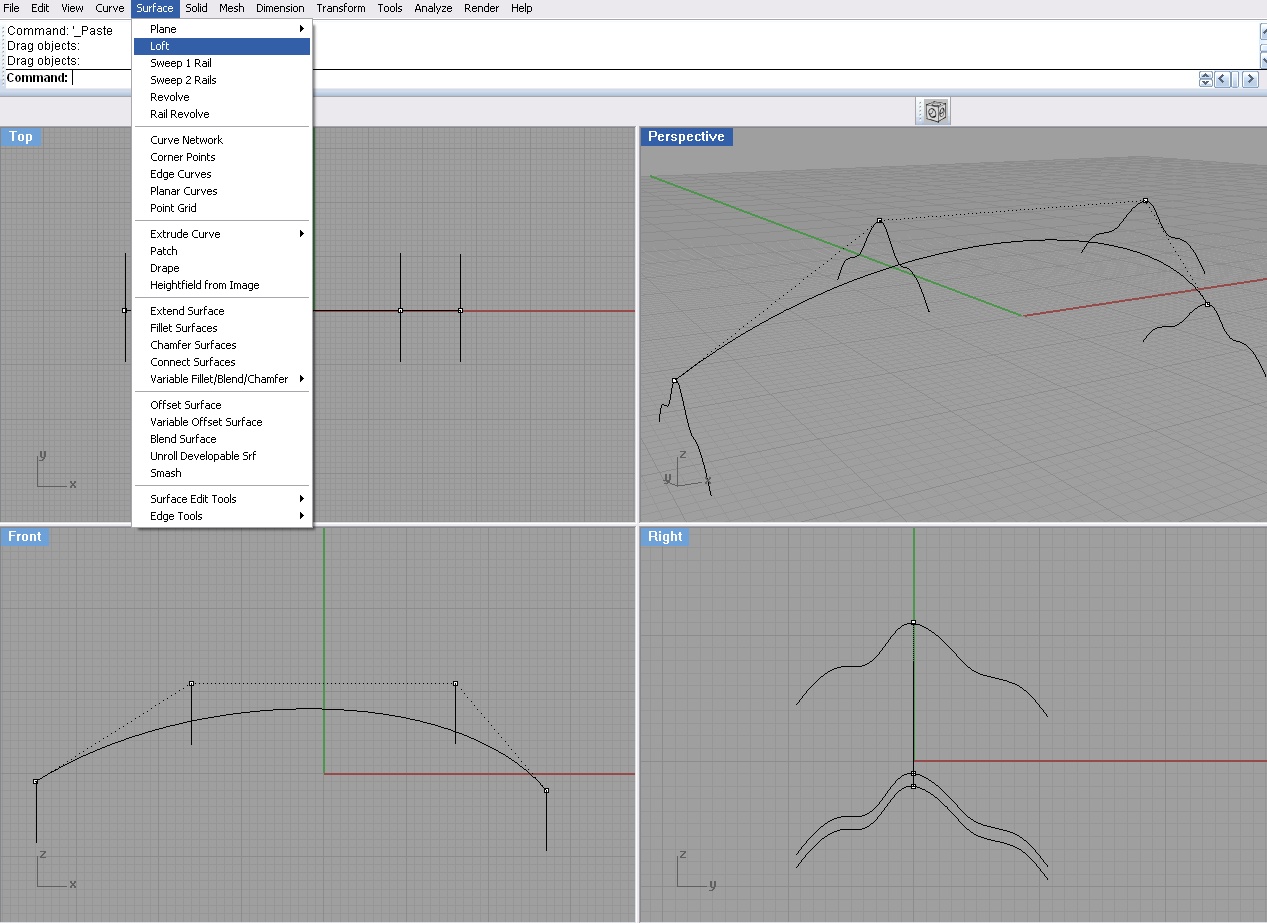
Co widzimy ? Otóż widzimy jak można ten sam kształt oddać za pomocą 8-krotnie mniejszej ilości danych.
Mam nadzieję, że się podobało. Na końcu zamieszczam scenę.
Aha, przykład zrobiłem na szybkiego, więc nie jest nic dokładnie do siebie ustawione, ani powierzchnie poprzez to nie są perfekcyjnie "identyczne", tak tylko na oko bo miałem 10 min na ten wpis.
Wątek: Zabawa w optymalizację (Przeczytany 8577 razy)